经典 Weierstrass 极值定理

本节我们会介绍一些基本定义和概念，包括什么是凸函数，什么是有界、闭合、紧致。同时我们还会回顾一些连续性的相关定义，以方便我们去证明后续的一些定理。

基本定义与定理

1. 有界 (bounded) ：有界集合有穷的集合半径；有界集合内部的任两个点的距离都是有穷的。
2. 闭合 (closed) ：闭合集合是有界的且边界在集合中的。
3. 紧致 (compact) ：紧致集合是有界的且闭合的。
4. 纯性 (proper)：纯度量空间内所有的闭合球 (closed ball) 都是紧致的。换言之，纯度量空间都是完备的(complete)。纯函数 (proper functions) 在自身非空的定义域中每个值都大于 $-\infty$ 且存在一个值小于 $\infty$。
5. 下半连续 (lower semi-continuous) ：闭合函数都是下半连续的，反之亦然。

\[f(x)\le\lim_{k\to\infty}\inf{f(x_k)} \qquad \forall x_k\to x \text{ and } \{x_k\}\subset X\]

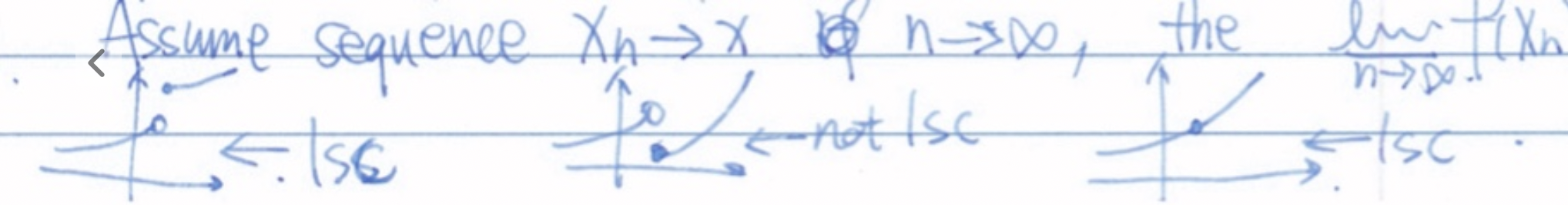
1. 强制性 (coercive) ：可以理解为是函数在轴两侧都是奔向无穷的。 \(\lim_{\\|x\\|\to\infty}f(x)=+\infty\)

2. Bolzano-Weierstrass 定理：任意有界的序列都有一个收敛的自序列。

极值存在定理

在证明 经典 Weierstrass 极值定理 之前，我们先推出一个初始版本的极值定理：

(定理 1) 对于一个 闭合，强制性的纯函数 (coercive, closed and proper function) $f:X\to(-\infty,+\infty]$，有 $(\exists x\in X) \text{ } f(\bar{x}):=\min f(x) = \inf f(x)$ : $\bar{x}$ 是函数 $f$ 的极小值点。

证明：

先定义一个序列 $(x_n)$ 让 $f(x_n)\to\inf f(x)$。

声明： $(x_n)$ 有一个有界的子序列。

（为了证明上面的声明是正确的，我们需要使用 反证法 来证明。这部分可能会有点绕）

假设 上面的的声明不正确，也就是说 $(x_n)$ 没有一个有界的子序列，则 $(x_n)$ 不是有界的。根据 强制性(coercive) ，对于 $\|x_n\|\to\infty$，我们有 $f(x_n)\to\infty$；

又根据我们对于序列 $(x_n)$ 的定义，$f(x_n)\to\inf f(x) = \infty$；这与纯函数的定义相悖。因此 假设 不成立，原命题 $(x_n)$ 有一个有界的子序列 为真。

由上面的推导，我们可以声明 $(x_n)$ 且有界。根据 Bolzano-Weierstrass 定理，$(x_n)$ 有一个收敛的子序列。我们在这里把这个有界且收敛的序列记作 $(x_n)’$。

因此我们有，

\[\inf_n f(x_n) \le f(\bar{x}) \le \underline\lim f(x_n)=\inf f(x_n) \qquad \forall x_n \in (x_n)'\]

其中，$\inf_n f(x_n) \le f(\bar{x}) \le \underline\lim f(x_n)$ 是根据 $(x_n)’$ 的收敛性和闭合性（由序列定义可知）

且因为 $\inf_n f(x_n)=\inf f(x_n)$，所以整个不等式就转换成了等式：

\[\inf_n f(x_n) = f(\bar{x}) = \underline\lim f(x_n)=\inf f(x_n) \ne -\infty\qquad \blacksquare\]

经典 Weierstrass 极值定理

上面的一些定理能够帮助我们去定义一个函数是否有一个极小值。在引出 经典 Weierstrass 极值定理 之前，我们还需要补充 指示函数 的一些定义和性质

1. 指示函数 （indicator function）：指示函数

\[\delta_C := \begin{cases} 0 & x\in C \\ \infty & x\notin C\\ \end{cases} \qquad \operatorname{dom} \delta_C = C\]

在面对指定定义域的问题时，可以结合指示函数来定义目标函数，比如 $f|_C$ 可以记作 $f+\delta_C$。同时我们可以注意到，$\delta_C$ 是一个闭合函数，

那么现在我们终于来到了本节的大 boss：

(经典 Weierstrass 极值定理) 对于一个下半连续 （lower semi-continuous）的函数 $f:X\to(-\infty,\infty]$ 在一个紧致的集合 $C$ 上， $\operatorname{dom}f \cap C \ne \phi$，那么 $f_C$ 有一个极小值。

证明：

首先我们面对由定义域的函数 $f|_C$，将其转化为 $f+\delta_C$。目标就是证明 $f+\delta_C$ 是闭合强制的纯函数，以利用之前证明的极值存在定理来证明这个定理。

（闭合性） 因为 $f$ 和 $\delta_C$ 都是闭合函数，我们先记 $f(x)+\delta_C(x) := (f+\delta_C)(x)$，那么有

\[f(x)+\delta_C(x)\le\liminf f(x_n)+\liminf \delta_C(x_n)\le \liminf \Big((f+\delta_C)(x)\Big)\]

所以我们可知 $(f+\delta_C)$ 是下半连续的，也就是闭合的。

（强制性） 当 $\|x\|\to\infty$，$(f+\delta_C)(x)\to\infty$。因为集合 $C$ 是闭合且有界的，所以超出闭合定义域的值会被指示函数顶到 $\infty$。

（纯性） $\operatorname{dom}(f+\delta_C) = \operatorname{dom}f \cap \operatorname{dom}\delta_C = \operatorname{dom}f + C \ne \phi$，所以纯性得到了保证。

因此函数 $f+\delta_C$ 是闭合强制的纯函数，根据极值存在定理，我们可以得到该函数存在一个极小值。$\blacksquare$

本节的内容就到这里，下一节我们会介绍凸函数，敬请期待～

返回所有博客 ｜ 返回首页