凸函数与 Hilbert 投影定理

本节我们会介绍凸函数和可分离定理。这是对于凸优化非常重要的基本概念。这为最优化算法可行性的判定提供了有效的依据。我个人也是觉得这部分算是容易理解并且很优雅的一节内容。

什么是凸函数

1. 凸函数的定义有两种形式：

   1. 定义：（类似地，我们可以来思考一下 凸集合的定义是什么？）

      \[f\Big((1-\lambda)x+\lambda y\Big) \le (1-\lambda)f(x) + \lambda f(y)\qquad \forall \lambda\in[0,1]\]

   2. Jensen 不等式：

      \[f(\sum_i\lambda_ix_i) \le \sum_i\lambda_if(x_i)\qquad\forall \lambda_i\ge0 \text{ and } \sum_i\lambda_i=1,\]
2. 凸函数的一些性质：

   1. （仿射不变性）：对于一个线性映射 $A:X\to Y$ 和向量 $b\in Y$，对于一个凸函数 $g:Y\to(-\infty,\infty]$ ，则 $f:X\to (-\infty,\infty]:x\mapsto g(Ax+b)$ 也为凸函数。

      证明：

      \[\begin{aligned}f\Big(\lambda x_1+(1-\lambda)x_2\Big)&=g\Big(A\big(\lambda x_1 + (1-\lambda) x_2\big) + b\Big)\\&=g\Big(\lambda Ax_1+(1-\lambda) Ax_2+b\Big)\\&\le\lambda g(Ax_1+b) + (1-\lambda)g(Ax_2+b)\\&=\lambda f(x_1)+(1-\lambda)f(x_2)\end{aligned}\]

      所以根据定义，可以证明凸性有仿射不变性。$\blacksquare$

   2. （非负权和下不变）：对于非负的 $\alpha_1,\alpha_2,\alpha_3,…,\alpha_m$ 和 扩充实值凸函数 (extended real valued function) $f_1,f_2,f_3,…,f_m$，那么 $\sum_i^m \alpha_i f_i$ 也是凸函数。

      证明： 这个证明很简单，推导一下就可以得到这个结果

      \[\begin{aligned}\sum_i^m \alpha_if_i\big(\lambda x_a+(1-\lambda x_b)\big)&=\alpha_1f_1\big(\lambda x_a + (1-\lambda)x_b\big) + \\&\qquad... + \alpha_mf_m\big(\lambda x_a + (1-\lambda)x_b\big) \\ &\le \lambda\alpha_1f_1(x_a)+ (1-\lambda)\alpha_1f_1(x_b)+ \\ &\qquad ... +\lambda\alpha_mf_m(x_a)+ (1-\lambda)\alpha_mf_m(x_b)\\ &=\lambda\sum_i^m\alpha_if_i(x_b) + (1-\lambda)\sum_i^m\alpha_if_i(x_b)\end{aligned}\]

      因此可得凸函数在非负的权重求和下，凸性不变。$\blacksquare$

   3. （凸函数集合的上确界为凸）: 对于一个凸函数集合 $(f_i)_{i\in I}$， 凸函数集合的上确界也是凸的。

      证明：

      \[\begin{aligned}\sup_i f_i\big(\lambda x_a + (1-\lambda)x_b\big)&\le \sup_i \big\{ \lambda f_i(x_a)+(1-\lambda)f_i(x_b)\big\} \\&\le \lambda\sup_i f_i(x_a)+(1-\lambda)\sup_i f_i(x_b) \qquad \blacksquare\end{aligned}\]

点到集合的投影

1. 支持函数（Support function）：支持函数 $\sigma_C(y):=sup_{x\in C}\langle y,x\rangle$，经过推导我们可以知 支持函数 是闭合且凸的。支持函数可以理解为绕着集合的一个函数，描绘了集合的边界。（当然这里我有点犯懒，我会补上这部分的证明的）
2. 支持函数的性质：（这里我们定义 $rA:=\{ra|a\in A\}$，$A+B:=\{a+b|a\in A, b\in B\}$（证明也是同上，我实在是太懒了）
   1. $\sigma_C(\alpha y) = \alpha\sigma_C(y)=\sigma_{\alpha C}(y)$
   2. $\sigma_C(y+z)\le\sigma_C(y)+\sigma_C(z)$
   3. $\sigma_{A+B}(y) = \sigma_A(y)+\sigma_B(y)$
3. 集合的投影（Projection of a set）：对于一个 非空且闭合的集合 $C\subseteq X$，对于一个任意点 $z\in X$，存在一个集合内的点 $x\in C$ 满足 $\|z-x\|=d_C(z)=\inf_{c\in C}\|z-c\|$。我们把满足这一条件的点 $x$ 定义为 集合 $C$ 的投影，记作 $P_C(z)$。

4. Dr Heinz Bauschke 戏称为 CUTE 性质 🤣：（其中 $\|\cdot\|$ 为 欧几里得范数）

   \[(\forall a\in X)(\forall b\in X)(\forall \lambda\in\mathbb{R})\\\ \|(1-\lambda)a+\lambda b\|^2+\lambda(1-\lambda)\|a-b\|^2=(1-\lambda)\|a\|^2+\lambda\|b\|^2\]

5. 如果 $\|\cdot\|$ 是 欧几里得范数，且 $C$ 为凸集合，那么 $P_C(z)$ 则是一个单点（singleton）。

   证明：先假设集合投影 $P_C(z)$ 有两个点 $x_0,x_1$ ，则有

   \[\begin{equation}\|z-x_i\|=d_C(z) \qquad i\in\{0,1\} \end{equation}\]

   我们先由凸性定义 $x_\lambda := (1-\lambda)x_0+\lambda x_1 \in C$，其中 $\lambda\in(0,1)$ 。因此有

   \[\begin{aligned}d_C(z)&\le \|z-x_\lambda\|^2=\|z-(1-\lambda)x_0-\lambda x_1\|^2\\&=\|(1-\lambda)(z-x_0)+\lambda (z-x_1)\|^2\end{aligned}\]

   根据上文提到的 CUTE 性质和上文两个点的定义，不难得到：

   \[\begin{aligned}Right &= (1-\lambda)\|z-x_0\|^2+\lambda\|z-x_1\|^2-\lambda(1-\lambda)\|z-x_0-z+x_1\|^2\\&=d_C(z)-\lambda(1-\lambda)\|x_1-x_0\|^2 \end{aligned}\]

   但是这里我们需要注意，$-\lambda(1-\lambda)\|x_1-x_0\|^2$ 是非正的。为了满足不等式 $d_C(z)\le d_C(z)-\lambda(1-\lambda)\|x_1-x_0\|^2$ 只能让 $-\lambda(1-\lambda)\|x_1-x_0\|^2=0$ 。因此证明了 $x_0,x_1$ 实际上是一个点，也就证明了若集合为凸，那么集合外一点到集合的投影唯一。$\blacksquare$

有了上面的凸集投影唯一的性质，我们就可以很方便地得到本节的主题：Hilbert 投影定理

Hilbert 投影定理

（Hilbert 投影定理）对于一个闭合的凸集合 $C\subseteq X,C\ne\phi$，任意不在集合内的点 $z\in X$，存在一个唯一的投影 $P_C(z)\in C$。同时，对于投影 $P_C(z)$，有 $p=P_C(z)\Leftrightarrow \langle c-p, z - p\rangle\le0$。

证明：因为集合为凸且闭合，$p$ 为集合的投影，因此我们有：

\[\|z-p\|^2\le\|z-\big(\lambda c + (1-\lambda)p\big)\|^2 \qquad \forall c\in C \qquad \lambda \in [0,1]\]

为了方便表示，我们定义 $a:=z-p,b:=c-p$ ，因此我们有：

\[\begin{aligned} \|a\|^2&\le\|a-\lambda b\|^2\\ \|a\|^2&\le\|a\|^2-2\langle a,\lambda b\rangle+\lambda^2\|b\|^2\\ 0&\le\lambda^2\|b\|^2-2\lambda\langle a,b\rangle\\ 2\langle a,b\rangle&\le\lambda\|b\|^2\qquad\forall\lambda\in[0,1]\\ \langle a,b\rangle&\le 0 \end{aligned}\]

我们重新带回两个定义，即可得到 $\langle z-p,c-p\rangle\le0$ 。$\blacksquare$

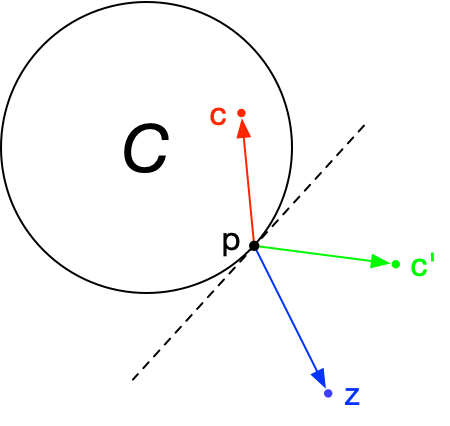
我们做了一个图示以方便大家理解。请大家看下图， $p$ 为点 $z$ 在集合 $C$ 的上的投影，对于在集合内的点 $c$ ，可以明显观察到 $\langle c-p, z - p\rangle\le0$ 。但是集合外的点 $c’$ 就不能满足上述条件。这样能让我们更感性地理解 Hilbert 投影定理。

有了这样优美的理论，我们总感觉还差点什么。就让我们引申一下，看分离定理是怎么推导的：

（分离定理）对于 $X\supseteq C \ne 0$ ，$C$ 是闭合的凸集合，点 $z\notin C$。那么， $\exists a\in X \backslash\{0\}$，$\exists\alpha\in\mathbb{R}$ ，满足 $\langle a,z\rangle>\alpha\ge\sup_{c\in C}\langle a,c\rangle$。

证明：定义 $a:=z-P_C(z)\ne0$ （因为 $z$ 不在 $C$ 中）和 $\alpha:=\langle z-P_C(z), P_C(z)\rangle\in\mathbb{R}$。 $\forall c\in C$，根据 Hilbert 投影定理，我们有

\[\begin{aligned}\langle c-P_C(z),z-P_C(z)\rangle&\le 0\\\langle c,z-P_C(z)\rangle&\le\langle P_C(z),z-P_C(z)\rangle=\alpha\end{aligned}\]

此外，

\[\begin{aligned} \langle a,z\rangle&=\langle z-P_C(z), z\rangle=\langle z-P_C(z),\big(z-P_C(z)\big)+z\rangle\\ &=\|z-P_C(z)\|^2+\langle z-P_C(z),z\rangle\\ &>\langle z-P_C(z),z\rangle=\alpha \end{aligned}\]

我们可以看到上面的没有不等式没有等号，是因为我们定义存在集合外的一点 $a$。$\blacksquare$

换言之，我们总能找到一个非零超平面 $\langle a,z\rangle>\alpha$ 将空间中含有集合 $C$ 的部分和不含 $C$ 的部分一分为二。

到这里本节的内容就结束了，下一节我们会简单介绍一下 次梯度（Subgradient） 的相关概念，请大家继续关注～

返回所有博客 ｜ 返回首页