向量搜索中的量化

鉴于最近向量检索比较热门，同时很多同学对于 ScaNN 的推导没有什么背景知识， 所以本篇内容主要来带大家复习一下什么是 Quantization 以及 Quantization 的一些作用。

暴力搜索对于查询大量数据（大于一百万条记录）而言非常奢侈。为了加速搜索、减少内存使用，常见的一些向量搜索（例如 FAISS）都会引入各种索引算法。今天我们就来详细介绍三个非常简单的索引算法。

Scalar Quantization (SQ)

如果说有一个 128 维 32 位 浮点向量，生成索引的最简单的拍脑袋方法就是把数据直接转换成一个 8 位无符号整数。 这个操作确实会带来一些收益的：首先这种索引减少了内存开销，另外计算无符号整数肯定比计算一个 IEEE 754 单精度浮点数要快的。

Vanilla Scalar Quantization (faiss::IndexScalarQuantizer)

当然如果直接运用上面描述的方法肯定是不可行的。想象一下如果是直接把一个值域在 -1 到 1 的向量转换成无符号 8bits 整型，那么获得的将是全损的向量（全部为零）。解决这个问题也相当简单，那就是在转换过程中先处理一下这些向量。假设我们有一个 $n$ 维的向量 $v \in \mathbb{R}^n$ ，那么我们的处理的过程可以这么描述：

\[v' =\sigma\big( \frac{v - \min(v)}{\max(v) - \min(v)}, 8\big)\]

其中，$\min(\cdot)$ 和 $\max(\cdot)$ 对应向量中最大值和最小值。$\sigma(\cdot, 8)$ 代表把浮点数转换为整型数的操作。这样就把一个比较连续的浮点向量转换为了离散的近似值。

如果将上面的方法推广一下，如果有 $k$ 个 $n$ 维向量，那么我们也可以保持上面的公式原封不动：使用 $V\in\mathbb{R}^{k\times n}$ 的最大值和最小值来量化所有的向量。这种方法对应了 FAISS 中的 QT_xbits_uniform。当然如果使用全局的最小值和最大值可能会影响量化的精度。因此我们可以使用 $\{\max(k)|k\in V^T)\}$ 和 $\{\min(k)|k\in V^T)\}$ 替换原来的 $\min(\cdot)$ 和 $\max(\cdot)$，也就是考虑每个维度上的最大值和最小值而不是全局的。这样就能显著提高量化的精度。这样的方法对应 FAISS 中 QT_xbits。

Marginal Equalized Scalar Quantization*

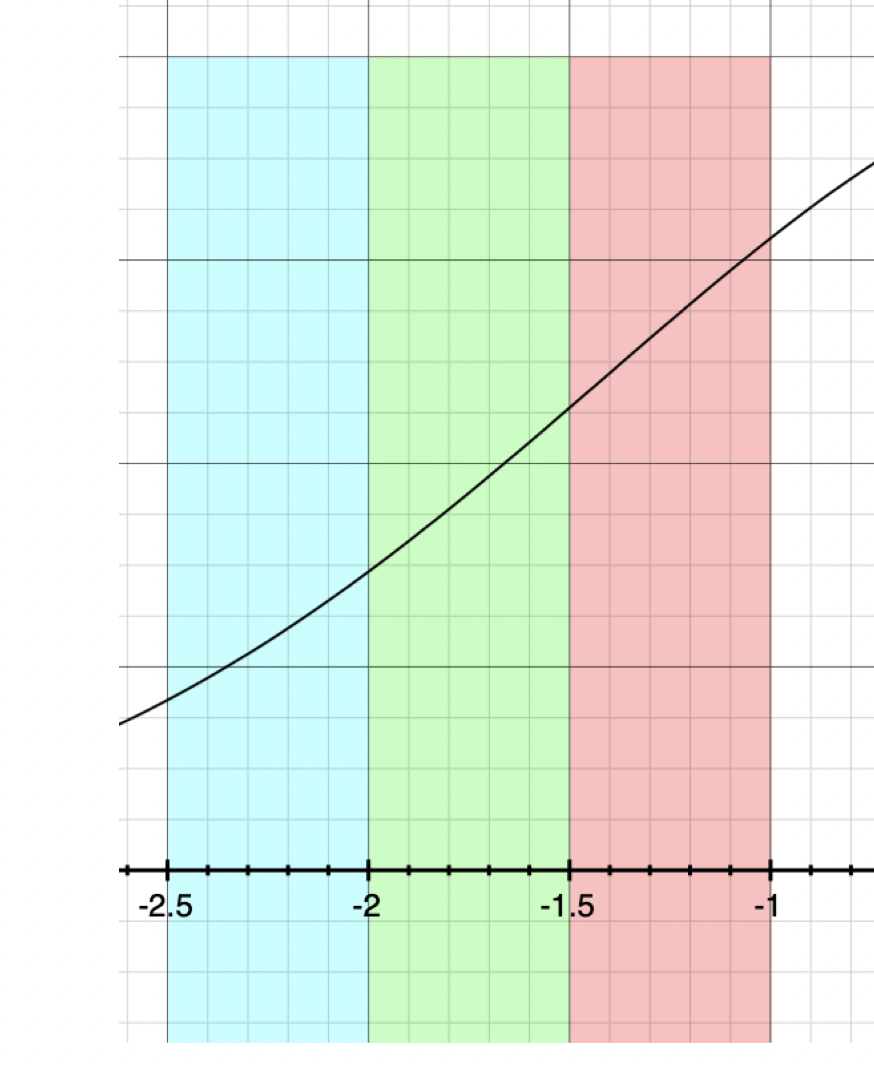
顺着上文的思路，我们整个的优化过程都是在改变如何获得取值范围，也就是在 min-max 上面做文章。但是从始至终，我们都没有对把浮点数转换为 $m$-bits 整型数的映射函数 $\sigma(\cdot, m)$ 进行任何的改动。我们实际上可以根据编码的密度来分配编码的区间。比如对于一个取值服从高斯分布的维度，编码区间在靠近均值附近应该比两侧更加紧凑。这样会比均匀的编码区间的重构误差小一些。

可以观察上图，带有颜色的等距条带代表着上文描述的编码区间。如果对于分布密度不均匀的编码（例如图中，曲线代表数值的分布概率），均匀的编码区间会让各个编码区间的出现频率不均衡。这会导致信息损失：数值出现频率更高的附近应该分配更多的编码，相对地数值更稀疏的部分应该分配较少的编码。这样能够确保经过重新编码的向量保持尽可能多的信息。

什么叫 Marginal Equalized Vector Quantization 呢？因为如果我们按照维度来统计直方图的话，都只是在统计边缘的编码分布，并没有考虑数据的联合分布。简单想象一下，如果是二维的分布，那么当前的边缘均衡的方法就不能轻松完成信息保留的目的。

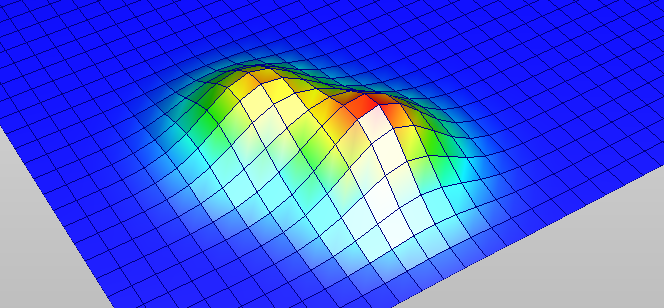
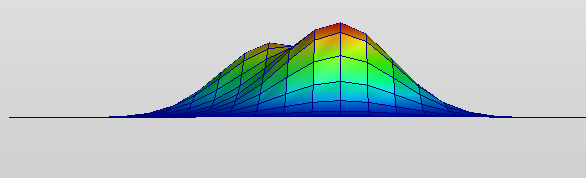
如上图的例子，我们如果使用边缘均衡化的方法量化，势必会将两个波峰中间的小谷编码区间变小，导致对应区域的分辨率升高。但实际上中间的分辨率并不应该变大，这会直接导致量化误差升高。如果进一步按照这个思路继续完善 SQ，那么就需要更完备的数学工具估计联合密度分布，并进行离散化编码。当然这是个还未完全开发的领域，期待着各位未来的创新！

Product Quantization (PQ)

在上面一节中，Vanilla Scalar Quantizer 并不能完全利用好整个的编码空间。为了改善这个问题，Herve Jegou （也是 FAISS 的第一作者）说我们可以换一种思路编码量化向量。Product Quantization 的名字顾名不思义，与我们理解的量化 Product （内积 什么的）没有什么关系（当然是我这样理解的）。其中的核心还是 proxy，就是寻找代替一群向量的 一个中心（Centroid）来代表这些向量。

Vanilla Product Quantization

原初的 PQ 思想其实不难从行文中揣测，就是使用 $K$-means 来寻找 $K$ 个 centriod 替代原有的向量。但是由于直接使用这些 centriod 编码开销过大，所以把这些全局的 centroids 拆分成各个 subspace 的 centroids 来替代全局的编码。首先我们来回顾一下 $K$-means。首先 $K$-means 里面的 $K$ 是指 $K$ 个中心，那么先假设有一个集合 $\mathcal{C} = \{c_1, c_2, …,c_K\}$ 。对于一个数据集 $X\in\mathbb{R}^{m\times n}$，我们可以把问题建模为

\[\mathop{\arg \min}_\mathcal{C}\sum_{i=0}^{K}\sum_{x \in X'_i} \|c_i - x\|\]

其中 $X’_i = \mathop{\arg \max}_{X’\in X, |X’|=n}{\sum_{a\in X’}\|c_i-a\|}$ ，也就是说 $X’_i$ 是 $X$ 中离 $c_i\in\mathcal{C}$ 最近的 前 $n$ 个元素。我们可以看到，这个问题实际上是一个 min-max 的优化问题。所以会被拆成两个步骤求解，文中的描述可以结合 Wikipedia 上的解释一并理解。

1. 赋值（Assignment）：类似于 Expectation，先求解 ${X’_i}_{i\in{1,2,…,K}}$​。在当前参数（中心集合 $C$）下估计前 $n$ 个的元素
2. 更新（Update）：类似于 Minimization，求解 $C$。求解在当前 ${X’_i}_{i\in{1,2,…,K}}$​ 下误差最小的 中心集合 $C$。

最基本的 $K$-means 介绍就到这里了。之后我们可以理解一下 $K$-means 在 PQ 中到底起了什么一个作用：

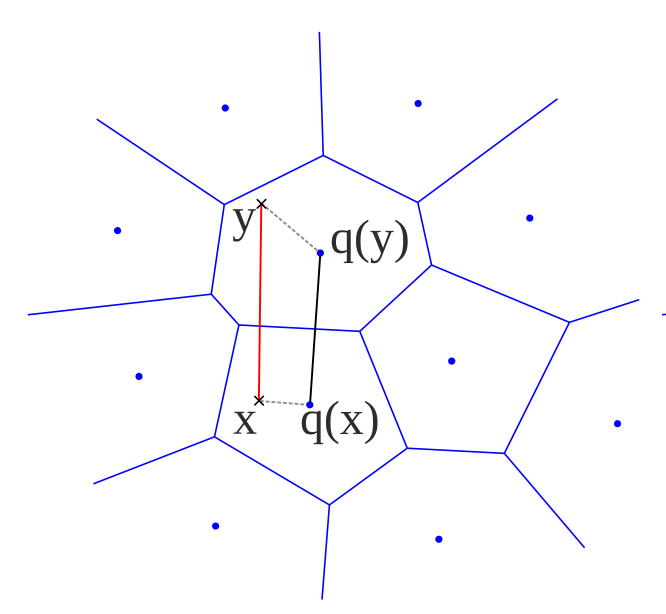
$K$-means 实际上会按照 Top-N 的边缘将空间切分为若干区域。由于 $K$ 时人为设定的，所以 PQ 可以使用这个参数来生成我们期望编码数量个中心。

将空间分成若干个区域（为了方便行文，我们先暂时把这些区域称作 cell）之后，我们就可以使用 cell 对应的中心来替代原有的向量。从而实现量化的效果。

当然读者们看到这里，实际上反映到 PQ 和 SQ 在核心思想上还是有连接的。SQ 希望编码更加均匀，而 PQ 希望编码能够根据向量本身的分布密度（Top-N 也可以看作是密度的倒数）来决定编码的方法。

当然事情到了这个地步，都还是没有 Product 的事情。所以说啊，起名字很重要。 那么我们来说说这个标题 Product。Cartesian Product（笛卡尔积） 的 Product 也是 Product。那么什么是 Cartesian Product 呢？我们学过数据库的大概都知道，SQL 里面有一个 JOIN 方法叫 CROSS JOIN。那么这个 CROSS JOIN 就是将两边集合的元素任意两两组合。比如有两个集合 $A=\{a,b,c\}$ 和 $B=\{e, f\}$，那么他们的 Cartesian Product 就是 $A\times B=\{a+e,a+f,b+e,b+f,c+e,c+f\}$。其中 $+$ 代表将两个元素合并。这个 Cartesian Product 可以产生两个集合中所有可能性的组合，所以反过来说可以将一个编码本（codebook）拆分为若干比较小的编码本。

从另一方面讲，一个欧式空间的子空间可以重构原有欧式空间的距离。所以我们可以直接使用下面的公式来得到他们之间的距离：

\[d(x,y)\approx d\big(q(x),q(y)\big)=\sqrt{\sum_{j}^{M}d^2\big(q_j(x_j),q_j(y_j)\big)}\]

其中 $M$ 就是切分的子空间个数。上面的表述方式是对称式距离计算（SDC）的方法。这样有一个好处，就是量化好的所有积都是提前计算好的，可以使用一个 LUT （Lookup Table）来加速计算。（实际上 SQ 也可以用这个 trick，所以这个 Product 实际上是个更广泛的方法）当然也有非对称式（ADC）的方法，可以这样用公式表述

\[d(x,y)\approx d\big(x, q(y)\big)\]

关于 SDC 与 ADC 的计算开销，原文有这样一个表格

好了以上就是 PQ 所有的内容了，接下来让我们看一下 Kaiming 在 2013 的这篇 OPQ 的工作～

Optimized Product Quantization

OPQ 顾名思义，就是可以优化的 PQ。那么本身 $K$-means 就是一个优化过程，我们还能如何加入优化呢？所以 OPQ 的作者们提出，我们可以回归一个线性参数 $R \in \mathbb{R}^{n \times n}$，把输入 $X\in \mathbb{R}^{m\times n}$ 重新映射一下。还记得我们在 $K$-means 的优化问题中把它拆解为两个步骤吗？我们在 OPQ 中 将原始向量做线性映射 $\hat{X}=RX$，把它再增加一个优化 $R$ 的步骤。

1. 赋值（Assignment）：类似于 Expectation，先求解 ${X’_i}_{i\in{1,2,…,K}}$​。在当前参数（中心集合 $C$）下估计前 $n$ 个的元素
2. 更新（Update）：类似于 Minimization，求解 $C$。求解在当前 ${X’_i}_{i\in{1,2,…,K}}$​ 下误差最小的 中心集合 $C$。
3. 优化 $R$，使得 $\mathop{\arg \min}_\mathcal{C}\sum_{i=0}^{K}\sum_{x \in \hat{X’_i}}\|c_i - x\|$，其中 $\hat{X’_i} = \mathop{\arg \max}_{X’\in RX, |X’|=n}{\sum_{a\in X’}\|c_i-a\|}$。

以上是 无参数化 OPQ 的内容。那么接下来我们再说一下 参数化 OPQ 的内容。有参数化的 OPQ 假设所有的数据都是遵从高维高斯分布。作者也指出，这种参数化的方法可以帮助无参 OPQ 生成初始值。

参数化的 OPQ 主要强调两个事情：第一个是 Independence；另一个是 Balanced Subspace Variance。那么怎么实现呢，答案是快 使用 PCA。

论文中使用了很多引理，不是很适合读者理解。不过从感性的理解来讲，相关性实际上就是多变量分布主方向的角度。PCA 能够给你一些正交的方向，这能够在确保一部分的独立性的同时保距（正交线性变换）。而平衡的子空间方差是通过对主成分重新排序来完成的。使用经过 PCA 转正以后的数据求方差，并对维度重新排序。按照大小为每个子空间分配维度。这样能够让子空间的方差更平衡一些。防止主成分扎堆导致中心描述能力下降。

以上就是 OPQ 的所有内容～

Residual Vector Quantization (RVQ)

近些年来还有一些残差量化的方法。其中的一些有点意思，所以捎带手也来介绍一下。

Additive Quantization（AQ）

与 PQ 思路不同， 虽然 AQ 也会把编码本分为 $M$ 组， 但是并不会把向量拆分开来。AQ 认为输入向量可以用 $M$ 个量化向量加和而来。如果也考虑编码时的方式，整个过程可以这样也就是说：

\[x\approx \sum_{m=1}^{M}c_m(i_m) \quad i_m\in\{1,...,K_m\}\]

其中 $K_m$​ 是 第 $m$ 个编码本的编码数量。在 AQ 原文里所有的$K$ 都是一样的。这种编码方法在速度上和 PQ 相差无几。对于一个给定的查询向量 $q$，$\langle q, x\rangle$ 可以提前以 codebook 中编码形式预先计算构建 LUT，之后再使用 LUT 快速查询。这个方法与 PQ 的 ADC 如出一辙。那么这么好的编码方式要哪里才能买到呢？

作者起手推导了量化误差 $E(i_1,i_2,…,i_m) :=\|x-\sum_{m=1}^{M}c_m(i_m)\|^2$。假设 $\|\cdot\|$ 是 L2 Norm，我们可以得到

\[\begin{aligned} E(i_1,i_2,...,i_m) &=\|x\|^2 - 2\langle x, \sum_{m=1}^M c_m(i_m)\rangle + \|\sum_{m=1}^M c_m(i_m)\|^2 \\ &=\|x\|^2 - \sum_{m=1}^M 2\langle x, c_m(i_m)\rangle + \sum_{m=1}^M \|c_m(i_m)\|^2 + \sum_{1\le m<m'\le M}2\langle c_m(i_m),c_{m'}(i_{m'})\rangle\\ &=\sum_{m=1}^M U_m(i_m) + \sum_{1\le m<m'\le M} V_{m,m'}(i_m, i_{m'}) + \|x\|^2 \end{aligned}\]

作者为了方便，记 $U_m:=2\langle x,c_m(i_m)\rangle$，$V_{m, m’}:=2\langle c_m(i_m), c_{m’}(i_{m’})\rangle$。以优化 $E$ 为目标的这个问题实际上是一个全联接的离散马尔可夫随机场的优化问题。作者提到了一些现有的方法，比如 Loopy Belief Propagation，这个方法 和 Iterative Conditional Modes 但效果都不是很好。最终作者使用了 Beam Search (一种启发式贪心算法）求解了这个问题。具体就是取队列，排序，贪心地放入队列，然后迭代的过程。

返回所有博客 ｜ 返回首页